Die Vedische Mathematik beschreibt Rechenregeln, mit deren Hilfe sich komplizierte Aufgaben blitzschnell lösen lassen. Hier ein paar Beispiele zur genaueren Erklärung.

Mathematik kann Freude machen. Besonders uralte Rechentricks lassen Schüler, wenn sie nur ein wenig geübt haben, zuweilen schneller als ihre Lehrer sein. Schneller auch, als wenn sie die Aufgaben in den Taschenrechner eingeben.
Inhaltsverzeichnis
Rechentricks der alten Inder
Die heilige Sprache der Inder, aus der sich unsere Sprachen entwickelt haben, war Sanskrit. Ein Vorgänger dieser Sprache ist Vedisch. Die Veden lebten um 2000 vor Christi Geburt da, wo heute die Inder leben. Sie entwickelten die Vedische Mathematik, welche im Jahre 1911 wieder entdeckt und 1965 veröffentlicht wurde.
Bei der Vedischen Mathematik handelt es sich um eine Rechenmethode, die manche Rechenprobleme recht einfach löst, da hier auf aufwändiges Herumrechnen verzichtet wird. Beschrieben wurden diese Rechenregeln, welche aus den sogenannten 16 Sutren und 13 Sub-Sutren bestehen, einst von Jagadguru Sankaracarya Sri Bharati Krsna Tirthaji Maharaja.
Ich möchte Ihnen die Vedische Mathematik nun einmal anhand von einigen Beispielen verdeutlichen bzw. etwas näher bringen. Also holen Sie nun Papier und Bleistift heraus, rechnen Sie mit und staunen Sie, wie einfach Vedische Mathematik ist.
Vedische Mathematik – So rechnen Inder
Die schwierigste Aufgabe im kleinen Einmaleins ist 7 x 8 = 56. Kleine Kinder sollten dies auswendig lernen, der Rest ist einfach. Mit der Kenntnis Vedischer Mathematik brauchen sie das aber nicht, denn das Einmaleins bis 5 x 5 reicht schon aus. Den Rest können die Kleinen oder auch Sie nämlich mit Hilfe der Vedischen Rechenmethoden im Kopf lösen.
Rechenregel: Vertikal und kreuzweise
» Rechenbeispiel 7 x 8:
Nach der Rechenregel Vertikal und kreuzweise schreibt man die Zahlen 7 und 8 untereinander und daneben die Zahlen, die bis zur Zehn fehlen, also 3 und 2. Jetzt wird kreuzweise subtrahiert, also 8 – 3 oder 7 – 2 = 5.
Daneben wird dann das Produkt aus den beiden vertikalen Zahlen 2 und 3 = 6 notiert. Beide Zahlen 5 und 6 nebeneinander geschrieben ergibt somit 56. Und das ist schon das Ergebnis!

» Weiteres Beispiel:
Nun rechnen wir 8 x 9. 8 und 9 untereinander, daneben 2 und 1, 8 weniger 1 oder 9 weniger 2 ist 7, daneben 1 x 2 = 2 und schon ist das Ergebnis 72 gefunden.
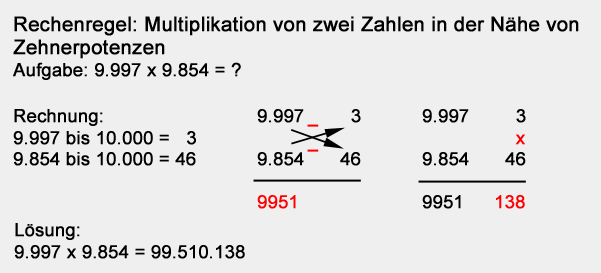
Rechenregel: Multiplikation von zwei Zahlen in der Nähe von Zehnerpotenzen
Bei größeren Zahlen geht das ebenso. In der Nähe von 10.000 liegen 9.997 und 9.854. Schreiben Sie die beide Zahlen untereinander, daneben die Zahlen, die bis 10.000 fehlen, also 3 und 46 und dann kreuzweise subtrahieren.
Daraus ergibt sich 9.951. Daneben nun 3 x 46 = 138 ausrechnen und schon ergibt sich das achtstellige Ergebnis, also 99.510.138.
» Weiteres Beispiel:
Wenn die beiden Zahlen ein wenig über einer Zehnerpotenz liegen, dann funktioniert das ähnlich. 102 und 121 schreiben Sie wieder untereinander, 2 und 21 daneben. Jetzt wird addiert statt subtrahiert, also 102 + 21 oder 121 + 2 = 123. Aus 2 x 21 ergibt sich 42, das Ergebnis ist also 12.342. So einfach ist das. Probieren Sie es mit anderen Zahlen aus und Sie werden sehen, wie einfach das geht.
Rechenregel: Quadrieren einer Zahl, deren hintere Ziffer eine 5 ist
Wenn eine Zahl auf 5 endet, dann lässt sich ihr Quadrat ganz einfach berechnen.
» Beispiel:
35 liegt genau zwischen 30 und 40. 30 x 40 = 1.200. Dazu addieren Sie 25, also ist 35 x 35 = 1.225. Oder 65 x 65 = 4.225, denn 6 x 7 = 42.
Die Veden hatten weiterhin entdeckt, wie einfach Zahlen in der Nähe solcher Zahlen multipliziert werden können. Wenn z.B. 65 x 65 = 4.225, dann ist 64 x 66 = 4.244. Die 42 errechnet sich wie oben aus 6 x 7, daneben schreiben Sie das Produkt aus 4 und 6 = 24 und schon haben Sie das Ergebnis von 4224.
Pythagoreische Zahlen
Pythagoras lebte um 550 vor unserer Zeitrechnung. Nach ihm ist der Satz des Pythagoras benannt, der besagt, dass bei einem rechtwinkligen Dreieck die Summe der Kathetenquadrate gleich dem Hypotenusenquadrat ist. Wobei die Katheten die beiden kürzeren Seiten sind.
Also:
3 x 3 + 4 x 4 = 5 x 5. Das gilt nicht für alle Zahlen, so gibt es keine ganze Zahl z für die gilt 4 x 4 + 5 x 5 = z x z. Andererseits gibt es unendlich viele Zahlen a, b und c für die gilt a x a + b x b = c x c.
Aber wie findet man solche Zahlen? Interessanterweise haben die Veden bereits 1.500 Jahre vor Pythagoras eine Rechenvorschrift entdeckt, mithilfe derer sich solche Zahlen finden lassen.
» Beispiel:
Sie müssen eine Zahl wählen, die zu den drei Zahlen gehören soll, beispielsweise 6, deren Quadrat ist 36. 36 ist durch 1, 2, 3, 4, 6, 9, 12, 18 und 36 teilbar. Jetzt wählen Sie davon zwei Zahlen aus, deren Produkt 36 ist, beispielsweise 2 und 18. Differenz und Summe der beiden Zahlen sind 16 und 20, deren Hälfte 8 und 10. Die drei gesuchten Zahlen sind dann 6, 8 und 10. Daraus ergibt sich:
6 x 6 + 8 x 8 = 10 x 10.
» Weiteres Beispiel:
12 x 12 = 144. Die Teiler von 144 sind: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144. Ich wähle 8 und 18 aus (8 x 18 = 144). Die Differenz und Summe der beiden Zahlen sind 10 und 26, deren Hälfte 5 und 13. Die drei gesuchten Zahlen sind dann 12, 5 und 13.
12 x 12 + 5 x 5 = 13 x 13.
Ich hoffe ich konnte Ihnen die Vedische Mathematik nun etwas näher bringen und wünsche Ihnen viel Freude beim Nachrechnen und Neuentdecken!
Videotipp
Für die sich die vedische Mathematik gern nochmal von Ranga Yogeshwar erklären lassen möchten:
Das könnte Sie auch interessieren:
» Notendurchschnitt ermitteln – 2 Varianten
» Kinder zum Lernen motivieren – 8 Tipps
» Nachhilfelehrer gesucht? – Mit diesen 5 Tipps garantiert den richtigen finden




